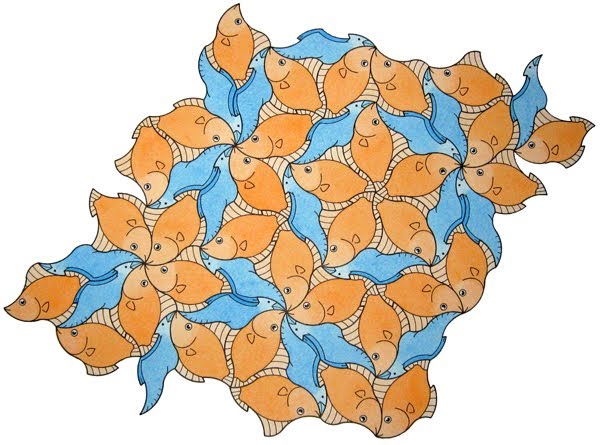
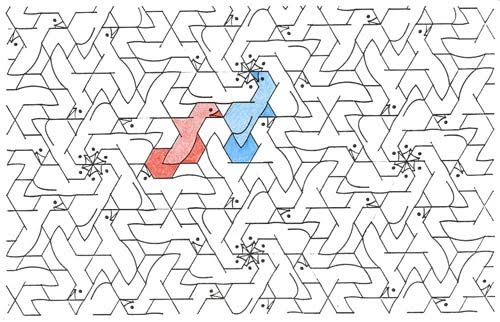
The title refers to tiles as devised by the British physicist Sir Roger Penrose (who has a keen interest in recreational mathematics), and as may be imagined, are somewhat more involved than with more 'ordinary' examples. More specifically, these are not one but two tiles that in conjunction tessellate in an non-periodic manner (hence their uniqueness), of which an excellent introduction, at a broadly accessible level, is to be found in an Scientific American article of January 1977 'Extraordinary nonperiodic tiling that enriches the theory of tiles'. A feature of these tiles for life-like motif purposes is that due to their non-periodic nature, each line has to represent four elements, this being in contrast to the 'normal' two of those without this aspect. Consequently, this makes the finding of quality life-like motifs most difficult. Two types are well known, of thin/thick rhombs, and kites/darts. Below I show an instance of the thin and thick rhombs. Another type is of a 'loaded wheelbarrow'.

Figure 2:
Detail

A 2.10 minute video with the tiles based upon the birds and fish above. This is by IMAmath (Institute of Mathematics and its Applications) and features the well-known Australian recreational mathematician, author, comedian, YouTube personality and communicator Matt Parker discussing the tiles. I might just add that I had no connection or knowledge of its making. Disappointingly, no reference is made to the bird and fish design, which ideally would have been made. The impression given is that the tile outlines are arbitrary (albeit within a Penrose context), rather than ‘special’, with the outline representing birds and fish.

'Loaded Wheelbarrow' Tile

A lesser known Penrose tiling is that of the 'loaded wheelbarrow', based on a single tile, so named by Martin Gardner (on account of its shape bearing a resemblance, albeit somewhat rudimentary) in an Scientific American article of August 1975 'More About Tiling the Plane: The Possibilities of Polyominoes, Polyiamonds and Polyhexes' in which a single tile is shown (this being set as a puzzle, with the answer and the tessellation shown in the next month's article).

The examples following show my efforts at forming life-like creatures with these. As such, these are generally of an inherently lower quality than with my normal standard, this being due to the tiles unique 'arrangement', in which a single line is repeated in a manner that is not conducive to the addition of life-like forms. This being so, their 'limitations' in this matter thus have to be accepted, albeit this should not be seen as an excuse for inferior examples.

This is based directly upon the 'loaded wheelbarrow', with the bird motifs of my own devising. Such an example is typical of the slightly lower standard as discussed above, as the bird motif is somewhat contrived, albeit remaining of a sufficient quality as to be worthy of inclusion.

Figure 3

Created 9 May 2014 as a single page. Originally 31 August 2009 as a series of sub-pages, of which I now amalgamate for the sake of a more succinct category.