Upon the completion of a finished work, as exemplified on the home page, this can be described as a ‘first generation’ parquet deformation. As such, this is all well and good and is perfectly acceptable as a finished work in its own right. However, for any one such finished parquet deformation, it is then possible to use this as a framework or springboard for a variety of further ‘second generation’ possibilities (of my own devising). The broad aim here is to see any trends/tendencies, both favourable and unfavourable (i.e. aesthetic and non-aesthetic), and then apply the favourable instances to other parquet deformations of a broad like nature. To this end, I use three different parquet deformations as exemplars, with the tiles being asymmetric, and one- and two lines of mirror symmetry. The format adopted is two-fold: first, I show the first generation parquet deformation, and second, the various 'extra possibilities' (as outlined above) as a second generation parquet deformation (as such, there can be one or more such second generation instances). Such a format makes clear the 'before and after' aspect at-a-glance. This involves applying standard mathematical symmetry operations to it, with overlays of translation, reflection and rotation. Typically, with the subsequent (second generation) symmetry operations, the parquet deformation becomes more involved, with a broad doubling of lines. As alluded to in a dedicated mini-essay on the subject, the computer is a great aid here and in such instances is where it really comes into its own, enabling the initial drawing to be used time and again, as against tedious successive drawing by hand which mitigates against experiment. In short, there is after all such a thing as a free lunch! The possibilities are just about endless, but the outcomes are not all aesthetic as another. Judgements must be made in the matter, otherwise the results become trivial. Although each of the examples shown here are practical by hand, much more can be accomplished by computer, in both speed of execution and design. Although the premise is easily stated, it is not perhaps as straightforward as may otherwise be thought to present in a consistent and ordered manner. First, there are the first generation parquet deformations. In themselves, these can be described as of symmetrical and asymmetrical tiles. And then for the second generation there is the matter of choosing a symmetry operation point; different places, e.g. vertices, mid-side, midpoint of the cell all have implications as to the outcome. And how should the analysis be set out? With so many variations, it is not easy! Therefore, the presentation given is subject to considerable revision. That said, it is ‘reasonably’ consistent for any one section. A ‘perfect’ presentation may never happen! The main point here is to outline some possibilities. Ideally, ‘all’ would be covered, but this reality is so difficult to accomplish that it may never happen! As is my usual policy, by far the best is to put something out (in a reasonable state), rather than wait for some ideal that may, or may not, eventually arrive, perhaps many years down the line. Note that the original study was undertaken (April 2021) amid a period of hectic analysis, for the purpose of possible inclusion (to some extent, greatly simplified) of my proposed piece in Werner Van Hoeydonck’s book. Therefore, it was simply not possible to be as thorough and all encompassing as I would have liked, with studies perhaps best described as an initial overview of the possibilities. Even though a relatively short time ago, I forget many of the intricacies here, and of which I have no desire to revisit. Rather, I will broadly simply let the old work stand, and suitably update the text, as well as improve in the round if I can. 1. SUBDIVIDING 1.1 Asymmetric Tile - Source (Tunisia - Sousse) 1.2 Symmetrical Tile, One Axis of Reflection - Source (Argentina - Buenos Aires) 1.3. Symmetrical Tile, Two Axes of Reflection - Source (Rio De Janeiro) 2. TRANSLATION 2.1 Asymmetric Tile - Source (Tunisia - Sousse) 3. MIRROR OVERLAY - HORIZONTAL AXIS 4. ROTATION OVERLAY - 180 1. SUBDIVIDING By suitably subdividing the tiles, new parquet deformations can be formed. A variety of lies are used, including diagonals, from left to right and right to left and then both diagonals. A particular favorite is a double basket weave structure. This gives a very pleasing overlay effect at right angles. Other subdivisions are less well defined, selected as according to the parquet deformation. The outcome can depend on the nature of the parquet deformation. For instance, some parquet deformations have asymmetric tiles, of mirror symmetry, or order 4 rotation, all of which impinge on the process as to aesthetics. To this end, I show examples of all three instances, with typical subdivisions. As can be seen, only a few can be described as aesthetic. 1.1. Asymmetric Tile - Source (Tunisia - Sousse)       1.2 Symmetrical Tile, One Axis of Reflection - Source (Argentina - Buenos Aires)  Fig. 2a. First Generation Parquet Deformation (Argentina - Buenos Aires)  Fig. 2b. Second Generation Parquet Deformation. One diagonal subdivided left to right (Argentina - Buenos Aires)  Fig. 2c. Second Generation Parquet Deformation. One diagonal subdivided right to left (Argentina - Buenos Aires)
Fig. 2d. Second Generation Parquet Deformation. Two diagonals subdivided, left to right and right to left (Argentina - Buenos Aires)  Fig. 2e. Second Generation Parquet Deformation. Double Basketweave (Argentina - Buenos Aires) 1.3. Symmetrical Tile, Two Axes of Reflection - Source (Rio De Janeiro)
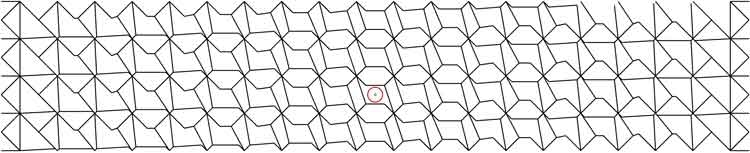
Fig. 3a. First Generation Parquet Deformation (Brazil - Rio De Janeiro)   Fig. 3c. Second Generation Parquet Deformation. One diagonal subdivided right to left (Brazil - Rio De Janeiro)   Fig. 3e. Second Generation Parquet Deformation. Basketweave 1 (Brazil - Rio De Janeiro) A beautiful design, with the pleasing feature of overlapping blocks of four tiles at right angles, in the same manner as the famous Cairo tiling.
Fig. 3f. Second Generation Parquet Deformation. Basketweave 2 (Brazil - Rio De Janeiro) Another beautiful design, with the pleasing feature of overlapping blocks of four tiles at right angles, in the same manner as the famous Cairo tiling. 2. TRANSLATION Fig. 4a. First Generation Parquet Deformation (Tunisia - Sousse)      Fig. 5b. Second Generation Parquet Deformation. Translation half unit, vertically (Argentina - Buenos Aires)  Fig. 5c. Second Generation Parquet Deformation. Translation mid cell (Argentina - Buenos Aires)  Fig. 6a. First Generation Parquet Deformation (Brazil - Rio De Janeiro)  Fig. 6b. Second Generation Parquet Deformation. Translation horizontally, half unit (Brazil - Rio De Janeiro)   Fig. 6d. Second Generation Parquet Deformation. Translation mid cell (Brazil - Rio De Janeiro) N.B. The alignment is (naturally) not exact, masked at this small scale of diagram. 3. MIRROR OVERLAY - HORIZONTAL AXIS Source (Tunisia - Sousse) Fig. 4a. First Generation Parquet Deformation (Tunisia - Sousse)  N.B. Reflected about vertex. The same outcome arises if a midside cell is reflected Argentina - Buenos Aires (Source)  Fig. 4b. Second Generation Parquet Deformation (Argentina - Buenos Aires) N.B. Reflected about vertex. The same outcome arises if a midside cell is reflected Brazil - Rio De Janeiro Fig. 5a. First Generation Parquet Deformation N.B. The same outcome arises if a midside cell is reflected  Fig. 5b. Second Generation Parquet Deformation N.B. The same outcome arises if a midside cell is reflected 3. MIRROR OVERLAY - VERTICAL AXIS Given that this symmetry operation results in the second generation parquet deformation being the same at both ends, this is lacking aesthetically, and is not to be compared to the 'standard model', where the tiles differ at the ends (this negates instances where the same tile arises, but through part of its natural cycle, which is aesthetic) Tunisia ADD Fig. 6b. Second Generation Parquet Deformation N.B. The same outcome arises if a midside cell is reflected
Fig. 7a. First Generation Parquet Deformation   Fig. 8b. Second Generation Parquet Deformation 4. ROTATION OVERLAY - 180 Fig. 9a. First Generation Parquet Deformation (Tunisia - Sousse)    Fig. 9c. Second Generation Parquet Deformation -180 around midcell (Argentina - Buenos Aires)    Old 13 April 2021) Upon the completion of the parquet deformation, which in itself can be considered as serving as a finished work, in effect a first generation parquet deformation, it is then possible to use this as a framework for further possibilities. This involves subdividing, and also superposing, using the three types of symmetry: translation, reflection and rotation. Typically, the parquet deformation becomes more involved, with a broad doubling of lines. In effect, such additional aspects can be described as second, third, and more generation parquet deformation forming. The possibilities are just about endless, but the outcomes are not aesthetic as another. Judgements must be made in the matter, otherwise the results become trivial. As alluded to above, the computer is a great aid here. Although each of the examples shown here are practical by hand, much more can be accomplished by computer, in both speed of execution and design. Subdividing By suitably dividing the tiles, new parquet deformations can be formed. Some are more obvious than others. A particular favorite is a double basket weave structure. This gives a very pleasing overlay effect at right angles. Fig. 1a shows a first generation parquet deformation, whilst Fig. 1b shows the second generation subdivision. Fig. 1a. First Generation Parquet Deformation  2. Translation - Superposition Superposition is another effect with pleasing visual properties. A variety of designs are possible, with a variety of different effects, depending upon the selected parquet deformation. Typical translations include vertical or horizontal slides of a half or one unit. Other possibilities include midpoints of the sides, as well as the midpoint of the cell. Fig. 2a shows a first generation parquet deformation, whilst Fig. 2b shows the second generation midcell translation.  Fig. 2a. First Generation Parquet Deformation  Page Created 31 August 2021 Note that the page is largely built on an existing essay of * 2021, mostly 'as is' posted on a generic essay page, as detailed above. The working Google document is titled ‘First and Second Generations 31 August 2021’. |
Parquet Deformations >
