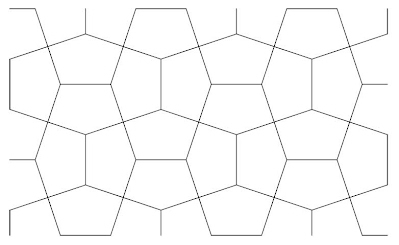
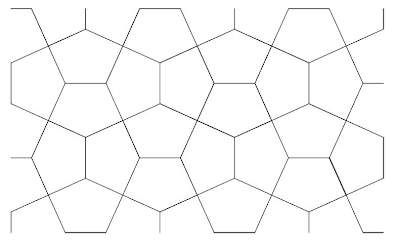
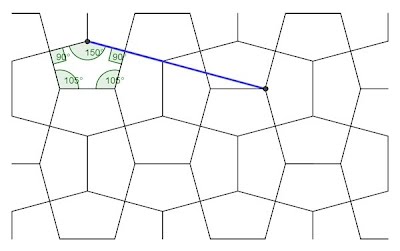
Although the Cairo tiling is well known and assumed by common consent, of a ‘standard model’ of a pentagon with adjacent 90° angles (invariable), of four equal sides, with a long or short base (variable) in relation to the sides, there are various problems with the variable and invariable aspects in defining a generic, catch-all Cairo tiling. Various authorities give a variety of ‘Cairo tilings’ that are not strictly of the in situ paving! Rather, the in situ model can be described as a single specific instance of a family of pentagon tilings that can be varied somewhat, in that the side lengths and angles are different, and yet still remain ‘Cairo-like’ in nature, although at its extremes this obviously departs seriously from the ‘standard model’. As far as I am aware, no authority has attempted such a catch-all instance, of which I now address. An obvious starting point is the in situ paving, shown below as a line drawing (Fig. 1). As an aside, this has properties of collinearity, not shown here. Figure 1. A line drawing of the in situ paving By its very nature, this naturally has all the attributes. However, as alluded to above, aside from the 90° angles, the other angles and side lengths are variable. In itself, this would not not normally cause a problem in that this can be simply described. For instance, Doris Schattschneider, a pentagon tiling authority, gave me this: ...the pentagon in this tiling is type 4 in the list of convex pentagons that tile the plane, characterized by the conditions that it has two non-adjacent angles that are 90 degrees, each enclosed by two equal sides. A stronger condition would be that all four of these sides are equal. As such, all well and good. This does indeed cover the ‘standard model’. However, it is possible to have a Cairo tiling in which all the sides are of the same length, i.e. an equilateral pentagon (Fig. 2), and of which this definition excludes. Therefore, the definition should include what can be described as this ‘special instance’. Building on the core description by Schattschneider, to accommodate the equialteral possibility I add: ??? But how best to do this? Figure 2. Equilateral pentagon tilingDoris’s definition seems to exclude the equilateral possibility (hence my addition). It's easy to tie oneself in knots accommodating this when it is ‘directly’ included. Perhaps it is better to retain the ‘...four of these sides are equal’ discussion, with reference to the equilateral sided pentagon as a special case, as an exception, after the main definition? How about two definitions, one suitable for a mathematical academic journal (for interest’s sake), and one more popular, suitable for Rawi, possibly mentioning mirror symmetry, which is only implied by Doris’s conditions; it may be obvious to the mathematician but not to the general reader! Although not directly related to definition matters, as above I have alluded to a family of pentagon tilings, below I show a table of such possibilities, in half degree increments, in which the pentagon in, various from maxima to minima, degenerating to squares and rectangle (the latter in a basket weave configuration), as first outlined by Robert Macmillan, in 1979. Some of these are of more interest than others, with special properties. For instance, No. 61 shows the dual of the 3.3.4.3.4 tiling (Fig. 3), whilst No. 46 shows the Cordovan pentagon (Fig. 4). The Cordovan pentagon has the interesting property related to collinearity in a way, when the parhexagon side is extended, it can be seen to alight on a vertex (a feature not typically seen). There is also another instance that also has an alighting on a vertex, No. 31, of which the pentagon does not seem to have been noticed before or have a title (Fig. 5)! May I be permitted to call it the Bailey pentagon? Figure 5. Bailey pentagonOf note concerning this 'simple' angle listing is that it does not include the in situ paving, which has more 'complex' angles, of 108° 43’ and 143° 13’. This also can be described as a 'special case', as it has the property of collinearity. Page created 26 June 2020 I might just ad that although I have previously composed a page with a similar title ‘Defining a Cairo-Type Tiling’, from 2013, this strayed from the core purpose, including a much broader definition, such as more than one pentagon, and even further loosening, that in retrospect although well intended, has serious concerns. However, upon revisiting the definition aspect recently, in connection with a forthcoming article for Rawi journal, of which a definition is to be included, and upon related correspondence with George Baloglou, one of my many collaborators in Cairo tilings matters, I once more revisited the problem. Although it may be thought to be simple, there are various intricases that militate against a simple definition. As ever, an open invitation to the reader. Does anyone care to give a defintion? |
Cairo Tiling >