or

Analysis of the In Situ Tiles as Regards Collinearity and Angles

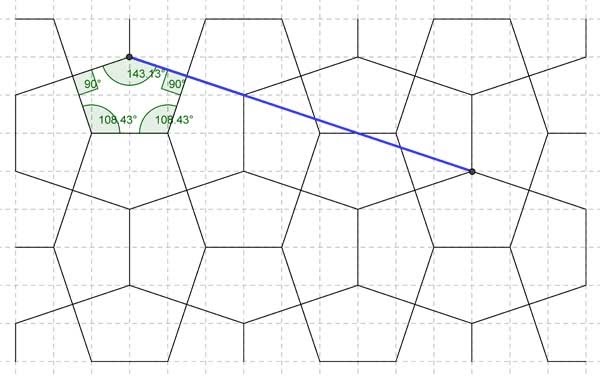
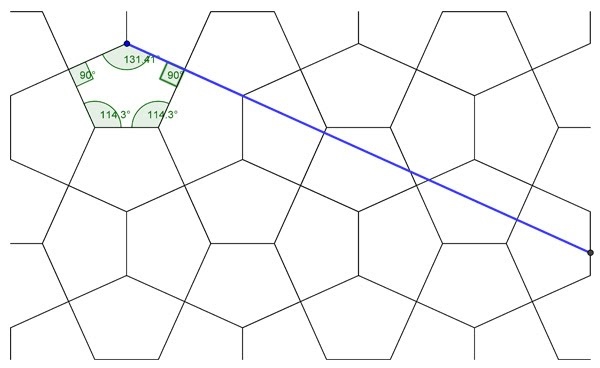
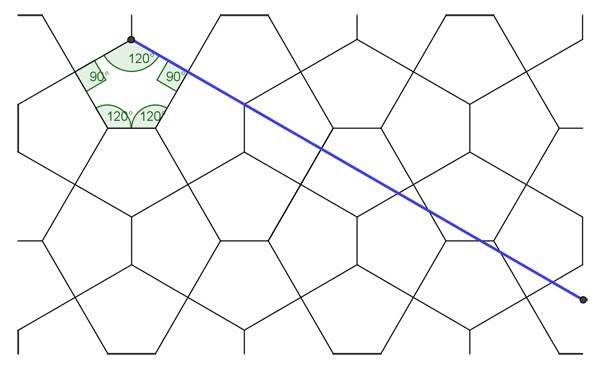
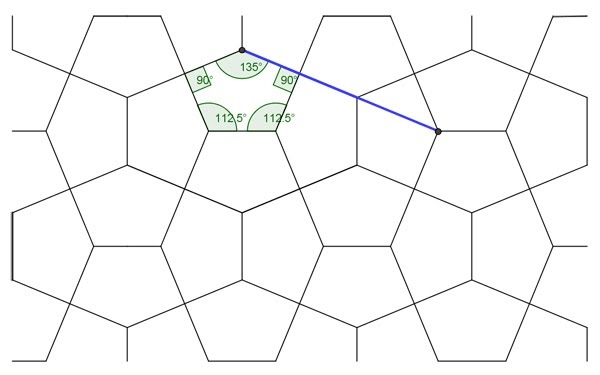
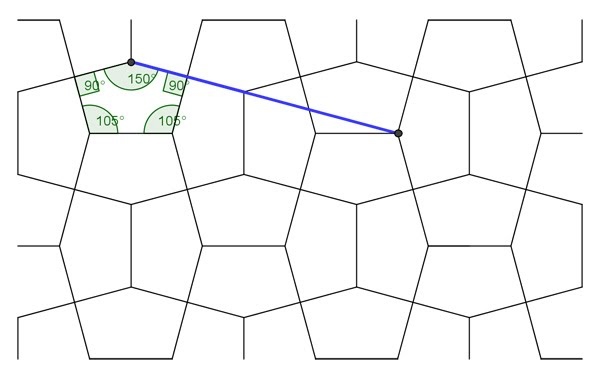
Introduction
An aspect of interest concerning the in situ pavings is the matter of their analysis, in regards of a collinearity condition as first reported by Robert H. Macmillan* (1921–2015) in his paper ‘Pyramids and pavements: some thoughts from Cairo’, in the Mathematical Gazette, December 1979, pages 251-255, and is of note as a first-hand account. Further, of interest as well is to what angles the pentagons actually are. This study thus examines both of these aspects, but concentrating on the collinearity aspect, of which in a sense they are to a certain extent intertwined. The collinearity reference by Macmillan is the first; it is not mentioned by James Dunn, in his earlier discussion (in the same journal) of 1971. This is possibly explained in that Dunn was under the misapprehension that the pentagon was equilateral, which it is not (and which this lacks collinearity, as shown below). Similarly, Martin Gardner based his discussion on the equilateral pentagon, from Dunn, and likewise does not mention collinearity. Likewise, in the same misattribution vein, Doris Schattschneider gives the model as 3.3.4.3.4, which again, does not possess collinearity. It was ever thus.... Incidentally, Macmillan appears to have been unaware of Dunn's account; he does not mention it. However, a major drawback is the presentation of his paper, it is unclear and vague in various places, despite some rigorous mathematics. It would have been interesting to hear of Macmillan's account from himself in person. To this end, I found contact details of him, resulting in a phone call in (?), but nothing was established. At this stage, he was quite elderly (*), and from another correspondent, Brian Wichmann, who first contacted him on the phone, found him hazy. I too found him hazy, and despite an invitation to visit his home in Milton Keynes, decided against it, believing nothing could be achieved. He sadly died in 2015. Of interest, really for the sake of curiosity, and nothing more, would be to know the circumstance and the date of Macmillan’s visit. The article does not detail this (not unexpectedly), merely stating ‘On a recent visit to Cairo I was struck by two matters…’ (referring to the pyramids and the tiling). Neither does the reference in Geometric symmetry, which he co-authored with E. H. Lockwood, his former teacher. Almost certainly given the date, this part came from Macmillan. Further, his Wikipedia page does not detail this, nor any other of his writings, although I have not examined ‘all’ here, or indeed even ‘most’. However, from the text, in which he gives ‘recent’, one can presuppose that the visit was in the last year or two of the publication, so say about 1976-1977. Perhaps in the earlier days of the investigation, with paucity of detail, such matters would be relative gold, but now are nothing more than of passing interest. Incidentally I am most impressed with Macmillan the man. His list of achievements, as given on the Wikipedia page, are most impressive. I am duly humbled.

Collinearity Premise
Of note is that in Macmillan’s paper, he refers directly to the in situ collinearity of the tiling:
P. 255, (iv):
(iv) If [symbol] is such that, in Fig. 4, AB and CD are collinear, the tessellation is especially pleasing to the eye, and this in fact is the proportion often* adopted in Cairo’
He then gives a mathematical explanation, in which he gives a pentagon with angles of 108° 26’ and 143° 8’ (I disregard the fixed angle of 90° here, as well as the figures repeating twice), albeit his presentation is not ideal, in that the diagram shown, Fig. 4 does not show this aspect, as well as there being no in situ pictures in the paper with overlays showing collinearity (or indeed any photos). However, Fig. 4 clearly lacks this property! Simply stated, I now believe Macmillan is referring to a possibility of such an occurrence, and not holding Fig. 4 as an exemplar. This is the crucial aspect. Therefore, the diagram is not in error per se. Essentially this thus sets the scene for collinearity, in which such a feature is established, if not entirely illustrated satisfactorily by Macmillan for reasons as above.

Collinearity Analysis
To examine this claim of the in situ photos, I this overlay appropriate lines over the photos of the two types of pentagons Figs. 1 and 2). A possible objection here, is that the 'perspective' photos do not portray the tiles orthogonality. However, I have been reassured by an early collaborator in my investigations, the mathematician John Sharp, that such overlaying remain valid, no matter the angle. Furthermore, due to the tiles being actual physical objects (rather than the geometer’s theoretical 'perfect' lines), and with these being artifacts put in place by the workmen not necessarily with the strictest degree of carefulness as regards the ‘perfect alignment’, especially of the square format type, the task of determining collinearity is thus made more difficult. Indeed, it can be seen that in some instances the proposed ‘correct’ collinearity is not seen, for this very reason. Therefore, one could thus quibble at being categorical here as to the existence of collinearity. However, these objections, in their various forms, can be overridden. As can be seen, the tiling does indeed possess the collinearity as espoused by Macmillan.

https://rechneronline.de/winkel/degrees-minutes-seconds.php

108°26’ converted to decimal = 108.43333. GeoGebra (decimal) gives 108.43 (two decimal places)

143°8' converted to decimal = 143.13333. GeoGebra (decimal) gives 143.13 (two decimal places)

Figure 5: Archimedean Dual (No Collinearity)

As such, with the collinear feature now firmly established, with all the in situ pictures possessing this feature, there can be no doubt whatsoever that the in situ pentagons were designed with collinear aspects in mind. Furthermore, as a corollary of this, as the commonly quoted examples of the equilateral or dual as being the Cairo pentagon do not possess collinearity, they cannot thus be the in situ pentagons!

Afterword

*Another interesting aspect to Macmillan’s work on this is an indirect reference to possibly the Cairo tiling again in his and E. H. Lockwood’s book Geometric symmetry, of 1978, page 88, of which the following discusses, somewhat as an aside or adjunct to collinearity. The closeness in the dates suggest that this is so. However, although specific as to types of tiling found, his account is frustratingly vague in terms of location, with

… the reciprocals of the tessellations 3². 4. 3. 4 and 3⁴. 6 are patterns of congruent pentagons such as often used for street paving in Moslem countries.

However, upon searching for such examples, I can find none. Given their relative simplicity, one would have thought that these would be common. The reference to ‘Moslem countries’ is decidedly vague; is he referring to Cairo, which would seem a fair supposition, given that he has clearly visited? Oddly, he makes no direct references here to the in situ pentagons as specifically described in his later pyramids and pavements 1979 paper, although he does refer to the 3². 4. 3. 4 tiling as a ‘special case’ there (amongst others), but apparently just as an abstract sense. However, possible support for this conjecture of such reciprocals existing is that amongst the in situ observations in the 1979 paper he gives, in regards to the Macmillan pentagon:

… and this is in fact the proportion often adopted in Cairo….

The operative word here is often, when he could have stated always. This suggests the possibility of variety. But perhaps I am reading too much into this choice of word; was this just a throwaway comment? It would now appear likely, given that there are no sightings of such types, and of the prevailing collinear types. Of note is that the in situ pictures are of same pentagon throughout, albeit in two different formats. What could explain this dichotomy? Likely, the above sentence, of a relatively lightweight nature, was just a relatively throwaway comment, this being in nature of decidedly less exhaustive account than with the 1979 paper. Therefore, I find it highly unlikely that these two reciprocals (duals) are to be found. But that said, why would Macmillan refer to these if he had no evidence? It’s all rather mysterious.

References

Dunn, James. ‘Tessellations with Pentagons’. The Mathematical Gazette, Vol. 55, No. 394 December 1971, pp. 366-369
Gardner, Martin. Scientific American. Mathematical Games, July. ‘On tessellating the plane with convex polygon tiles’, pp. 112-117 (p. 114 and 116 re Cairo aspect), 1975

Macmillan, Robert H. Mathematical Gazette, 1979. ‘Pyramids and Pavements: some thoughts from Cairo’, pp. 251-255.

Schattschneider, Doris. Mathematics Magazine, January. ‘Tiling the Plane with Congruent Pentagons’, pp. 29-44 (p. 30 re Cairo aspect).

https://en.wikipedia.org/wiki/Robert_Macmillan

Page History

7 October 2011. Page created.

15 May 2020. Clarification and correction as to why I believed the Macmillan and Bailey pentagon were 'different' added as a single paragraph, effectively appended to the page upon the Piker finding.

22 June 2020. In the light of the Piker finding, upon reflection, I decided to drastically rewrite the page, omitting much speculative material regarding Macmillan aspects that had become outdated, especially in regards of what were believed to be two different pentagons, albeit of slight difference. Further, I removed some line diagrams involving the thickness of the grooves drawn in GeoGebra. And added 'Angles' to the title, to better reflect the dual nature of the study. However, although much changed, the page is still broadly recognizable of the first incarnation.