Aesthetic Cairos

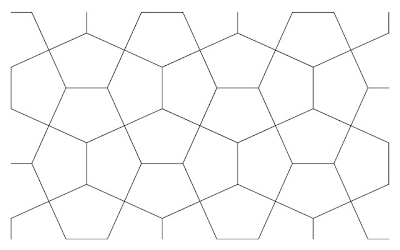
Introduction

As can be seen by the various studies, there are a multiplicity of examples that are, loosely defined, as ‘Cairo-like’ (with a pentagon of two non-adjacent angles that are 90°). However, aesthetically, these differ, some of these are ‘better’, or are of more interest, due to their inherent mathematical properties. This page thus collects these, and examines their properties.

1. Equilateral pentagon (114° 18’, 131° 24’)

Fig.1

Aesthetically this is very pleasing indeed, and arguably this is the ‘best’ pentagon in the series, not only here of the 1 pentagon category but the series as a whole, in that it is the most ‘basic’ of all the pentagon types, in that it possesses the most symmetry, namely of all five sides the same length, of which I consider the overriding issue as regards aesthetics. (The other examples in the series here can be described, at least in comparison, as weaker, with different side lengths). Indeed, this is my own personal favourite. Such aesthetics probably account for its popularity as the frequently stated serving model, likely from Gardner’s account (MacMahon also gives this). However, it does posses one relative shortcoming, in that it does not possess collinearity of others, namely.
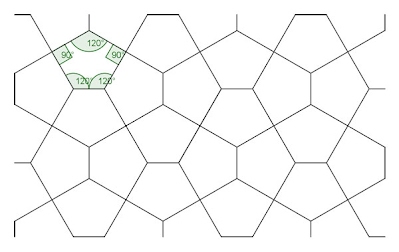
Also, to me at least, (but of very much of minor importance), is that upon a ‘broad, casual glance’, it has the pleasing appearance of a ‘faux’ regular pentagon tiling, despite this being known not to tile.

2. Dual of the 3². 4. 3. 4 (120°)

Fig. 2

Aesthetically this is very pleasing indeed, and arguably, the second ‘best’ pentagon in the series, due to its underlying background, namely that of the dual of the semi-regular 3².4. 3. 4 tiling. However, I consider that it pales aesthetically, in relative terms, as when compared with the equilateral, in that the major shortcoming is the sides lack those all of the same length. (In contrast to the equilateral pentagon, the sides not of the same length, with four of these being the same, with one decidedly ‘short’ in relation to the other four, described as of the ‘4, 1 short’ type (in contrast to ‘4, 1 long’, to others which is also possible) But that said, due to its underlying source it still has much aesthetic value. Furthermore, it has ‘pleasing’, round figure, ‘aesthetic’ interior angles, two of 90°, and three of 120°, something which the other ‘core value’ examples lack. Also lacking is collinearity. Another factor in its favour is that it is of a 'average' pentagon, the mid point between the minimum (rectangle) and maximum (square) conditions as set out by Macmillan.

Again, as above with the equilateral, likely on account of its many aesthetics, many authors cite this as the defining model.

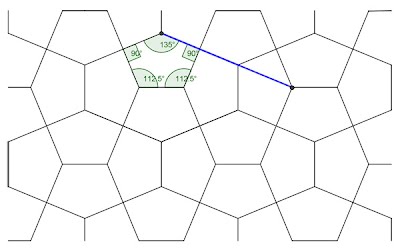
3. Cordovan, by Redondo and Reyes (112.5°, 135°)

Fig. 3

4: Bailey (105°, 150°)

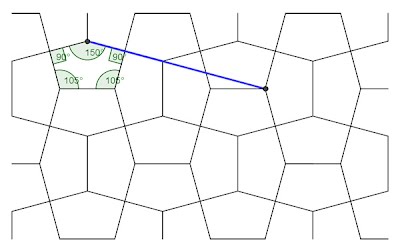Fig. 4

Aesthetically pleasing, with a collinearity feature; when the sides are so produced it results in the ‘nearest neighbour’ pentagon in a like orientation intersecting at a nearest vertex. However, in matters of collinearity I still consider the side collinearity as a superior aspect. Surprisingly, this particular pentagon is apparently completely known, found by myself amongst my Cairo studies, hence the attribution.
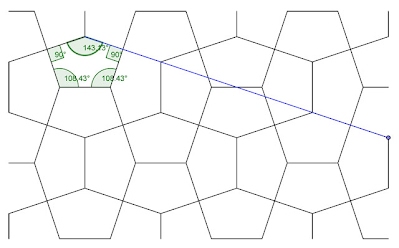
This is somewhat alike in premise to the Cordovan example above, and essentially echoes its premise, in that it possesses the property not of collinearity of sides but of intersection, as when the sides are produced it results in the ‘nearest neighbour’ pentagon in a like orientation intersecting at a far vertex.

5. Squared Intersections (108° 43’, 143° 13’)

Fig. 5

Aesthetically, this is pleasing in regard as to the general resemblance to the serving model, and indeed is the strongest of its type; at a casual glance, they are indistinguishable. Indeed, as discussed elsewhere, this could possibly serve as the in situ model, with Macmillan having been mistaken. This example, based on the reflected stick figure premise, is remarkably like the in situ example, with convex pentagons, with near like angles (contrast 108° 26’, 143° 8’), same side proportions (4, 1), with collinearity, with convex subsidiary hexagons and a long base. Note that further examples of a similar stick cross premise/construction lack such close angles and this collinearity aspect.

This possesses most of the properties of the serving model, namely symmetrical, two 90° opposite angles, 4: 1 ratios, subsidiary convex par hexagons at right angles, collinearity, and a long base (the latter in relative terms). Indeed, it has all the same attributes!

Created 1 June 2012

Comments