With a premise of a repeating tiling, most Escher-like tessellations
consist of relatively few motifs, typically one or two, and less frequently,
three, four, or more motifs. Indeed, five and higher are next to unheard of, at
least to any degree of quality, due to the increase in numbers of motifs, which
as a rule mitigates against quality. However, one can indeed increase the
number of distinct motifs in a tessellation by relaxing the premise of the
repeating element, but still retaining the tessellation aspect of ‘double
contour of outline’, with what I term (or more precisely, borrow from Escher’s
terminology) as a ‘Free-Plane filling’ tessellation, of which for the sake of
consistency I retain. The basic model for this is Escher’s ‘free plane fillings’,
I and II, of 1951 and 1957, with 36 and 39 respective different motifs. Both
are ‘typical Escher’, with animal motifs, some recognisable, some more fanciful
than others, and indeed some of an ‘extreme nature’, with pure fantasies, and with
just the one inanimate exception, a guitar. As can be seen, this tiling does
not repeat in any way, but in principle at the extremities it could be
continued with other motifs. An open question is to how
difficult this kind of tessellation is to achieve; is it is very difficult, perhaps
only possible due to Escher's capabilities, denied to lesser mortals, or is perhaps,
in relative terms, easy after all? At first impression it would appear highly
difficult, but, as other people show below, bearing in mind the all important
quality aspect, this is not so, this type is well within the capabilities of any tessellator of worth. That said, a
series of largely formless, ‘suggestion of nothing’ shapes is simply not good
enough. As usual, Escher has led the way, and set the scene for his successors,
of which it can be seen that the premise is not particularly difficult to
accomplish.
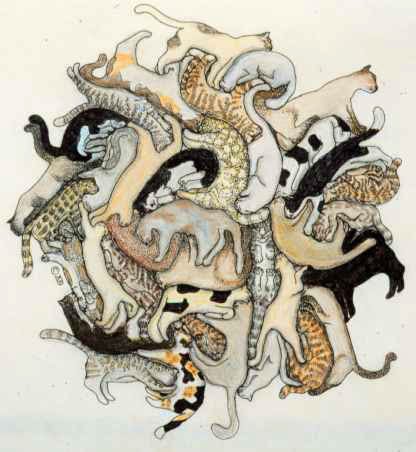
Two instances other than Escher are particularly worthy of note, by Bobby Bogl and A. K. Dewdney. Interestingly, both of these people are little known in the Escher-like tessellation world, and indeed, their interest in Escher-like tessellation appears confined to examples of this kind, all of which suggests that this type is not particularly difficult. Both of these people are different in style. Bogl includes both animal and inanimate motifs, combined, in roughly equal proportions, and furthermore shows more than a single example, showing three compositions. Dewdney concentrates on animate forms, and although all are of animal motifs, is more restrictive in his choice of motif, namely with cats only, with one instance. Both are interesting in their own respective ways, of which I now discuss. Bobby Bogl Bogl shows three instances, of Interlocking Everything, Tessepuzzlation, and Karaoke Tessellation. All three instances are very much alike in style, but are each undoubtedly distinct, and posses a wide variety of motifs, both inanimate and animate, and pleasingly of high quality (and furthermore, ‘balanced’, in that there is an approximate 50/50 division with animate and inanimate motifs). As can be seen, these are very nicely rendered, almost to a photorealist degree. Indeed, one has to search very hard to find any serious distortions here, which is credit to the artist (Escher's two instances contains many). Of note is how generally ‘strong’ these are in silhouette and not just formless shapes with decoration much beloved by other inferior tessellation artists. Although there is the odd example of the lower degree of difficulty of ‘heads’ here, this is almost inevitable, and should not be looked upon as an inherent weakness. All in all, all three are very pleasing compositions indeed. A. K. Dewdney Dewdney shows a single instance, Cats, of 37 motifs. As such, this is praiseworthy due to the theme and quality. The theme (of one particular motif) does not allow for variation so much as the type as espoused by Escher and Bogl, in that it is obviously more restrictive, and yet despite this Dewdney has an instance of high quality. This is easily seen as high quality, as the cats adopt a series of typical different poses, with the silhouette largely easily recognisable, and so these are not merely cat decoration features added to a formless shape. As can be seen, without the restriction of a duality of line at the edges of the composition, this enables the cats to be even more lifelike here, and as such is noticeably ‘looser' at the extremities than with Escher's model. All in all, very pleasing composition indeed. © A. K. Dewdney M. C. Escher Escher shows two instances, titled Free Plane Filling I (1951) of
36 motifs, and Free Plane Filling II
(1957). Escher’s instances are of interest due to these all being animate in
form, with one exception, of a guitar. Indeed, the inclusion of a guitar seems
incongruous amongst a sea of animate forms. Better would simply to have
excluded this, in favour of a consistent approach. Both of these instances are very
much alike in style. The motifs are mostly of a fantasy nature, with at times
noticeable distortions, without any pretence as to an existing real-like motif.
The very nature of this thus begs the question of quality. Is using fantasy
motifs ‘acceptable’, in the broader sense? One could argue that it is not, or
at least is less challenging. Certainly, by any standards, this must be judged
as easier than Bogl’s and Dewdney’s implied ‘restrictions’ of using only
true-to-life motifs and theme.
Of interest is the border; Escher more or less retains the framework of the underlying tile ‘construction’, of quadrilaterals (of I); in contrast Bogl and Dewdney are more ‘looser’. Note that this is not a criticism of the latter, but more of an observation. All in all, as a generalised statement, I consider Escher’s instances to be inferior to Bogl and Dewdney. Although Escher once again pioneered this type, this does not necessarily mean that this is to be considered as the best on that basis alone. George Paulus Another apparent instance is by George Paulus, an American architect, as detailed in Visions of Symmetry (page 306), who in 1963 sent Escher his own composition of this type, but so far as I know this is unpublished. Unfortunately, I have not been able to find further details of this work of Paulus. Does anyone know of this work or indeed of him? Summary As alluded to above, both Bogl and Dewdney are little known, indeed if at all, in the Escher-like tessellation community, and so such instances, coming from essentially ‘outsiders’, therefore suggests that ‘free plane filling’ as a type is not particularly difficult (but as ever, with the proviso of the quality issue), but this is a moot point. On the one hand, although the tessellation principle remains, one has considerably greater choice, in that the underlying tile is not ‘fixed’, and so there is more opportunity for ‘success’ to happen. However, this offers new challenges not caused by a ‘normal’ tessellation, in that in such a composition there are more instances of ‘duality of line’ that have to be addressed. Therefore, the difficulty of this should not be understated. An open question is to why none of the world’s top, or indeed lesser tessellators have not done this. Personally, I have previously thought it to be lacking any real challenge, as the relaxed conditions permit motifs of no particular difficulty (note the preponderance of fantasy type creatures in Escher’s instances, in which their outline permits plenty of leeway. However, this is not to unduly deride this type of tessellation. Indeed, I consider that I (and indeed others) have been neglectful here. Not to undertake at least one of this type in one’s oeuvre is simply overlooking an interesting ‘variation’ of the tessellation premise. And furthermore, as both Bogl and Dewdney show, one can have thematic instances, and so this alone offers additional scope for innovation. What about a ‘free plane filling’ of birds only, fish only, etc. What about entirely animate/inanimate? What about an entirely fantasy instance? There is scope here for considerable innovation. If anyone feels to be so inspired as so be inclined to try their hand at this, or already has an example of this that is of some degree of quality, I would be more than interested in hearing from you, and placing any examples here. Also, of one’s views on the premise of the concept, whether you have undertaken this or not; is it indeed difficult or easy? Created: 6 April 2012 |