So, upon having determined the number of individual colourations, I now turn my attention to their implementation, with 4 x 4 blocks, with the intention of determining 'all encompassing' colourations, that is all possible map-colourations of 1-, 2-, 3-, and 4-colours. However, such an ideal, although apparently simple in its remit, is not readily determined.
So, where to begin? The study as shown is composed with the benefit of hindsight, and is not the original one of my notebooks. As such, it is impractical to post the whole study on the web, as it consists of the equivalent of a c.200 page book. Therefore what follows is a concise version, albeit still thorough in intent. Certainly, nothing of note has been omitted. As a broad principle, where for example a large set of 4 x 4 blocks exist, I show the first few members, in effect establishing the principle, rather than including all.
Firstly, I begin by examining what I term as 'special cases', thereby permitting an idea of the depth of what the problem entails. This takes the form of compiling those examples possessing what I term as 'ultimate symmetry'. This is defined as in all instances, for the Block of 4, this entails distinct colourations without any repeats, of 'even distribution'. As such, this is decided, selective, choice, as permissible colourations that do occur that are not shown, due to the above condition. Ideally, this should be shown, as a 'wider category' (and is discussed in part 3), but if so included here then the colourations increase considerably, and so in this instance are not considered.
The method used is one of compiling stages, using quadrants, as shown below.
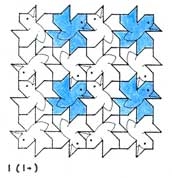
For each of the family members derived from the individual colourations, of 1-, 2-, 3-, and 4-colourations these are then shown as for each stage. However, as this is a somewhat lengthy study, instead I establish broad principles, in which for the first example I show in full (Stages 1-4), followed by the end product of the other examples without the intermediate stages i.e. the complete 4 x 4 blocks.
1-Colouring, Stages 1- 4
Stage 1 - a Set of 1
Stage 2 - a Set of 3
Stage 3 - a Set of 6
Stage 4 - a Set of 6
The 2-, 3-, 4-Colour 4 x 4 blocks
Having established the stage construction principle above, rather than repeat 'unnecessarily', Stages 1-3 for the 2-, 3- and 4-colourings are instead shown without the intermediate stages (1-3), as Stage 4 blocks.
2-Colour
Type A
Type B
Insert pic
Type C
Type D - Set of 18
Type E Set of 4
Type F Set of 4
diagram below is distincts - note difference!
Type G Set of 4
3 Colour
Type A Set of 2
Type B Set of
Insert pic
Type C Set of 2
Type D Set of 6
Type E Set of 2
Type F Set of 6
4 Colour
Type A Set of 5
Now, upon completion, a possibility is that due to the colours appearing in mutiple ways, the blocks from any one grouping may consist of the same intrinsic colouration i.e. identical. To check for such examples, I now analyse in an abstract manner, by using numbers. Each colour is given a number, with Blue, Green, Yellow and Red now 1, 2, 3, and 4 respectively.
Again, for reasons of conciseness, I am somewhat selective, only showing those examples where identicality is a possiblity. Interestingly, some ambigous results as regards distinctness occurs for both 1- and 2 colouring only. Although this may seem to be a simple question as to answer, perhaps even below worthy of attention for those people of the of the Tiling listserver, I nonetheless state my case.
Beginning with the simplest, of 1-colouring (below), it can be seen that the abstract colouration can be applied to all six examples, thereby implying that all six are intrinsically identical. Indeed upon so doing, then such a claim can be made. However, upon visual inspection, then a different claim can be made. Block 1 (1+2+3+4) can be seen to have blue and red bird motifs to be non contigous, these being diametrically opposed. However, Block 2 (1+2+4+3) has red and blue bird motifs contigous. In this instance, I thus show that the two diagrams are thus distinct. Therefore, two distinct arguments can thus be made for inherent identicality. However, both cannot be right, so which is it?
1-Colouring Abstract Analysis, Type A
add pic
A like situation arises for the two-colouring examples. Interestingly, each member, of Types A-G has a partner. Such an occurence disposes me towards the case that these (all members) are thus repeats i.e. not all distinct. However, doubts remain.
2-Colouring Abstract Analysis (Type A only shown, for reasons of conciseness)
|