Stick Cross Drop Method  Premise This method retains the premise of stick crosses of studies 1-2, but with the notable difference in that this is not confined to a square or rectangular matrix, nor indeed reflected. Here, the stick crosses are placed as according to the orthogonals of the squared paper, with the premise of allowing the crosses to ‘drop’. As a consequence, this gives a most interesting Cairo-like tiling with the following properties: 1. One pentagon only 2. The number of 90° angles can vary, from two (mostly) to three (few), the latter being a ‘special case’ (involving, or what can be interpreted as a Greek cross) As can be seen, this slightly ‘weakens’ the premise of the typical Cairo-type, in that the tiles, with the exception of the ‘special case’ is no longer symmetrical, but is still worthy in my opinion of the designator ‘Cairo-type’. Tilings 2 Unit Stick Cross Examples As these are
of the infinite type, of necessity I restrict the drawings to the first few
gradient types. Broadly, a few suffice to show the general principle, and so as
they are labour intensive to draw, for reasons of time saving, further examples
are not shown. To establish the principle of sequence, the 2 unit stick cross examples are shown in more depth, with the others a 'first representative'.  Gradient 1:2, symmetrical pentagon, 2 different sides, 3, 2, special case 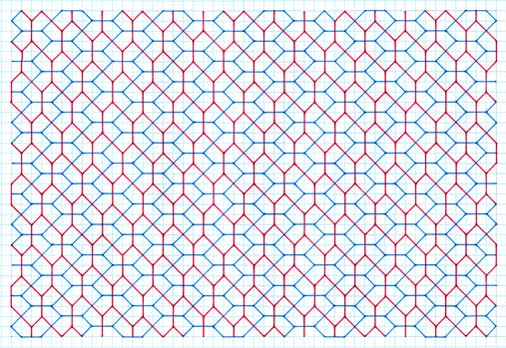 Gradient 1:3, symmetrical pentagon, 2 different sides, 3, 2, special case 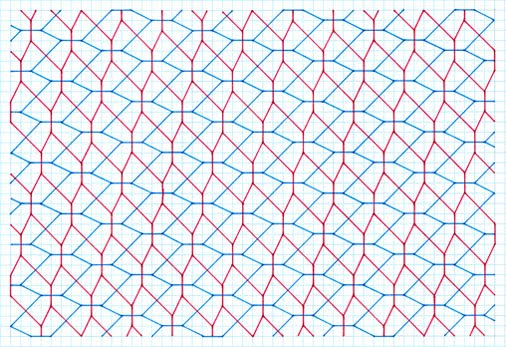 Gradient 1:4, asymmetrical pentagon, 3 different sides, 2, 2, 1  Gradient 2:3, asymmetrical pentagon, 3 different sides, 2, 2, 1  Gradient 2:4, asymmetrical pentagon, 3 different sides, 2, 2, 1 4 Unit Stick Cross Examples 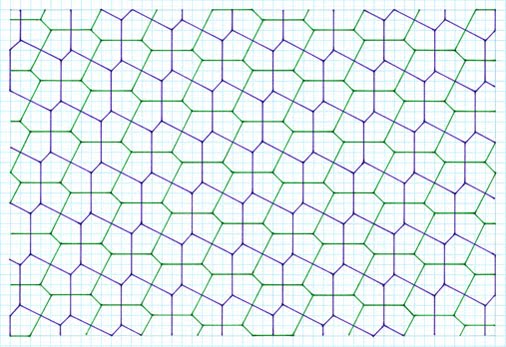 Gradient 1:5, asymmetrical pentagon, 3 different sides, 2, 2, 1 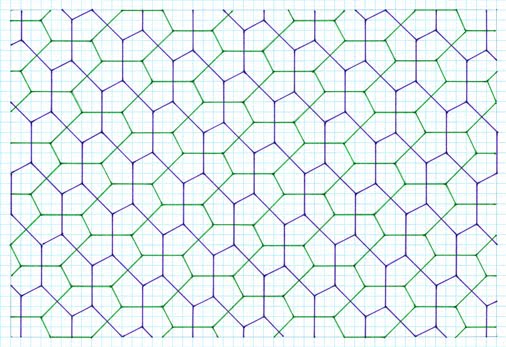 Gradient 2:5, asymmetrical pentagon, 3 different sides, 2, 2, 1  Gradient 3:5, asymmetrical Pentagon, 3 different sides, 2, 2, 1 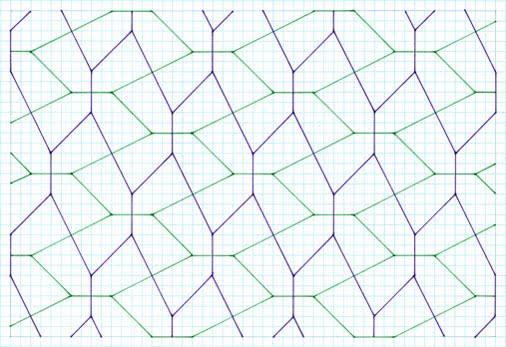 Gradient 4:8, asymmetrical pentagon, 3 different sides, 2, 2, 1 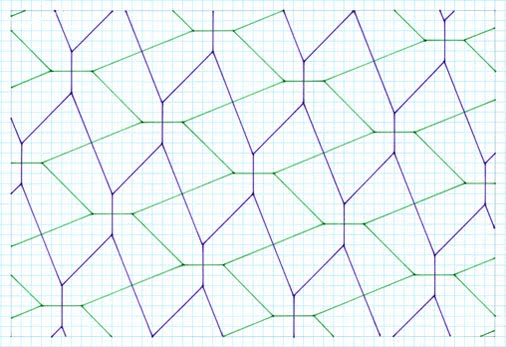 Gradient 5:9, asymmetrical pentagon, 3 different sides, 2, 2, 1 6 Unit Stick Crosses 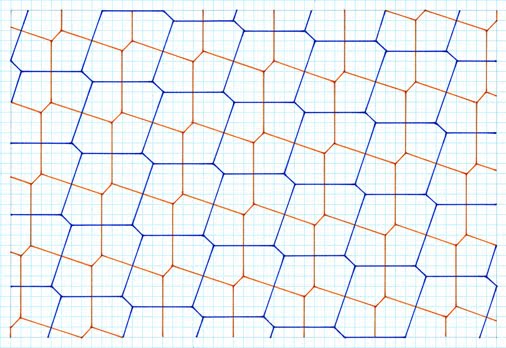 Gradient 1:7, asymmetrical pentagon, 3 different sides, 2, 2, 1 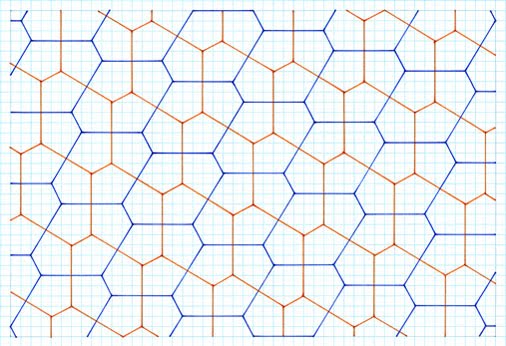 Gradient 2:7, asymmetrical pentagon, 3 different sides, 2, 2, 1 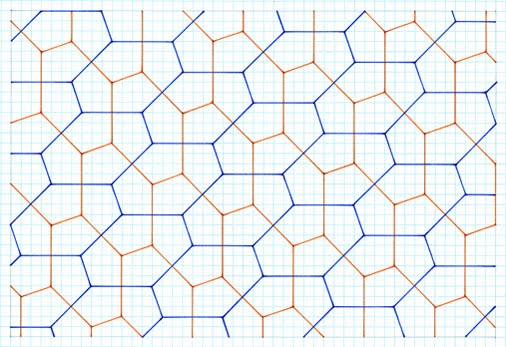 Comments Variation This method retains the premise of stick crosses of arms of the same lengthas above, but with the notable difference of different arms in combination, such as 2 and 4 units, , with the same premise of allowing the crosses to ‘drop’. Tilings  2 and 4 units, gradient 1, 4 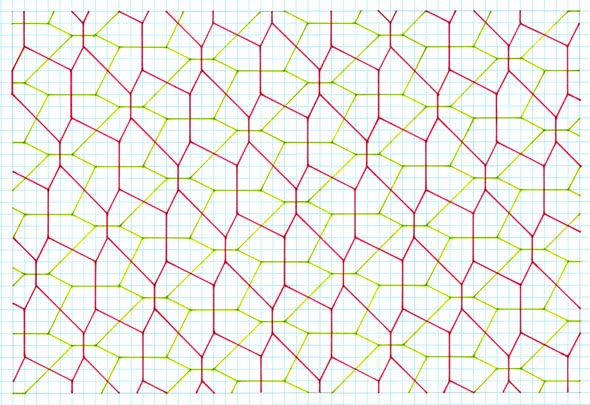 2 and 4 units, gradient 1, 5 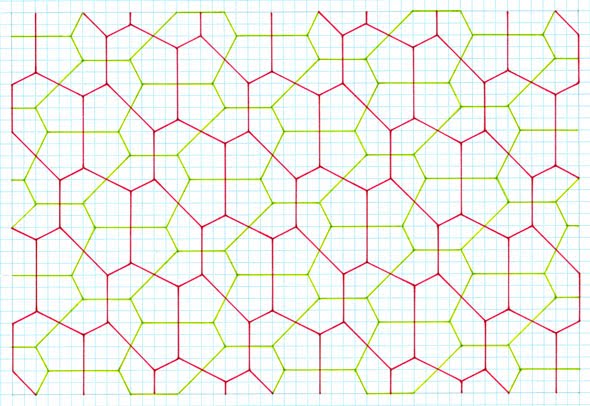 Comments As can be seen, this procedure gives rise to two different pentagons. Although
these are not symmetrical, they nonetheless give cause of interest. Perhaps of
most note is that the subsidiary hexagons are now no longer par for all three
sides; only one is. As can be seen, this slightly ‘weakens’ the premise of the
typical Cairo-type (i.e. of subsidiary par hexagons), in that the tiles are no
longer as aesthetic with all sides par hexagon, but instead are obviously more
irregular. However, even with this weakened ‘feature’, they are still worthy in
my opinion of the designator ‘Cairo-type’, and in any case are of interest in
their own right. One interesting feature of these is the distribution of the
pentagons, in that the like pentagons are ‘contiguous’, rather than at opposite
ends of the subsidiary hexagon as occurs with other, non-related example Another Variation Premise Tilings 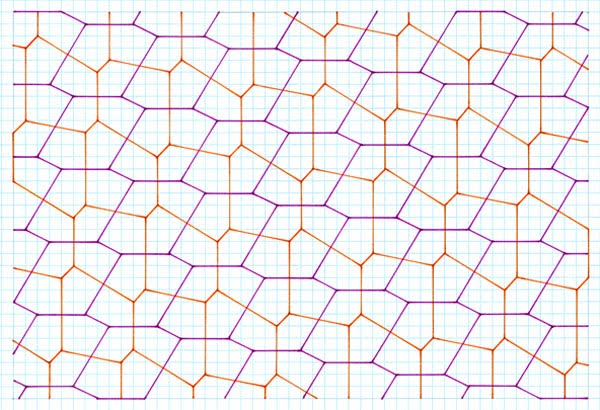 4 asymmetrical pentagons; 4, 4 and 4, 6 units, gradient 1:6, two subsidiary hexagons, one wholly par, the other just one side 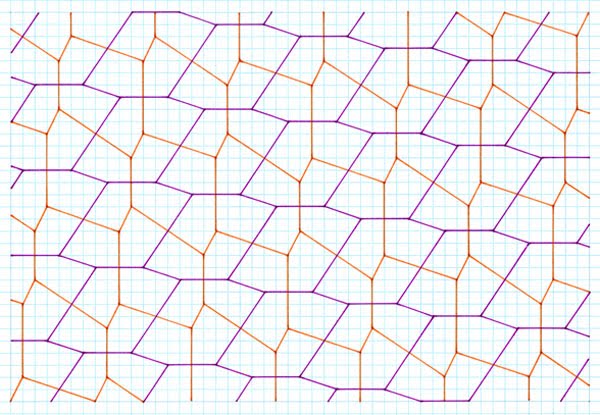 4 asymmetrical pentagons; 4, 4 and 4, 6 units, gradient 1:7, two subsidiary hexagons, one wholly par, the other just one side 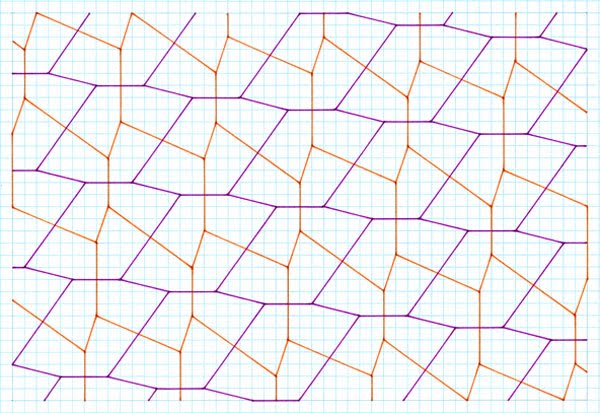 4 asymmetrical pentagons; 4, 4 and 4, 6 units, gradient 1:8, two subsidiary hexagons, one wholly par, the other just one side 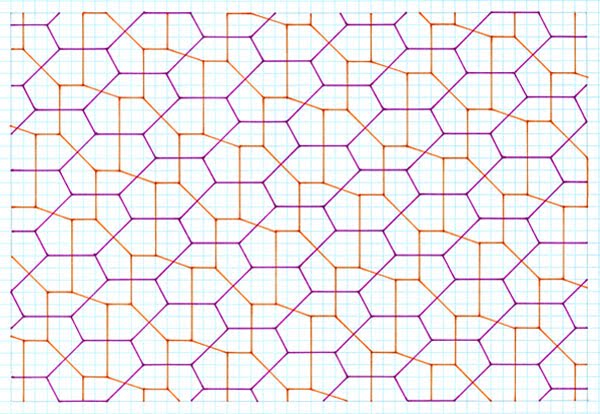 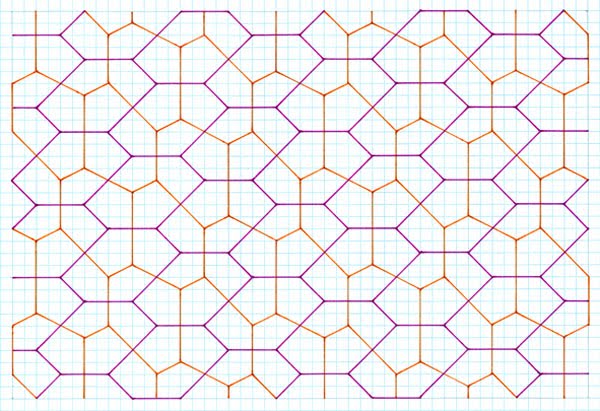 Comments As can be seen, this procedure gives rise to generally four different pentagons, although three pentagons are to be found in a single ‘special case’ (which requires investigation at a later day). Although the four pentagons are not symmetrical, they nonetheless give cause of interest. Perhaps of most note is that the subsidiary hexagons are now no longer par for all three sides; only one is. As can be seen, this slightly ‘weakens’ the premise of the typical Cairo-type (i.e. of subsidiary par hexagons), in that the tiles are no longer as aesthetic with all sides par hexagon, but instead are obviously more irregular. However, even with this weakened ‘feature’, they are still worthy in my opinion of the designator ‘Cairo-type’, and in any case are of interest in their own right. Of note is that this is yet another example of an ‘infinite’ type of composing, of which those shown is just a sample of the first few. As can be seen, the pentagons arising (and subsidiary hexagons) are the ‘same’ in all instances, from which one can extrapolate that all others must be of the same type i.e. topologically the same, with the exception of the ‘special case’. Another aspect to this is one of interpretation, in that although the tilings were produced by stick crosses on a gradient, another interpretation of this is of par hexagons with subdivision, although this interpretation is open to scrutiny, in that the hexagons are not simply translated as regards the interior division, but rather translated and rotated. |