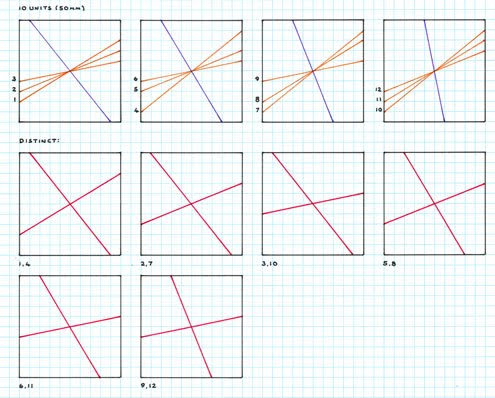
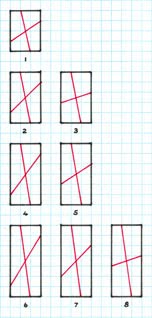
Premise This continues with the ‘reflected stick
cross’ premise as in Study 1, but here, rather than a symmetrical cross of
equal arms in a square matrix as according to the intersections of the unit
grid, I instead consider an asymmetric
cross. As can be seen, this divides the square matrix into four different
regions, two of which are distinct, and so consequently when the square matrix
is reflected it thus gives two
different pentagons. As can be seen, the pentagons are symmetric, of 2, 2, 1
side lengths for any given tiling. Of note is that the angles are no longer 90°. The pentagons range from being two
of very much alike to widely different ones, with decidedly short and long
bases, of which incidentally can this be described simply as of short or long
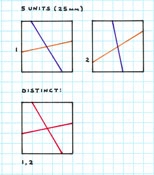
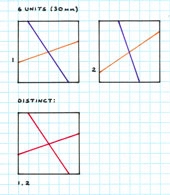
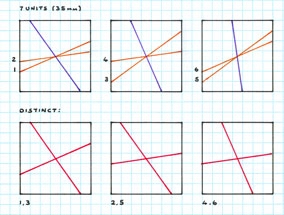
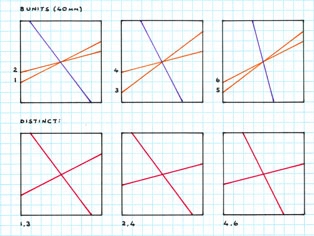
bases. Examples of 5-10 unit squares are shown, a five unit square being the
minimum, of which this as this is another example of an ‘infinite’ type, of
which I cease at 10 units, with 20 distinct examples, this being more than
sufficient to see the ‘nature’ of the eventual tiling
5 x 5
6 x 6
7 x 7
8 x 8
9 x 9
10 x 10
Set of 20
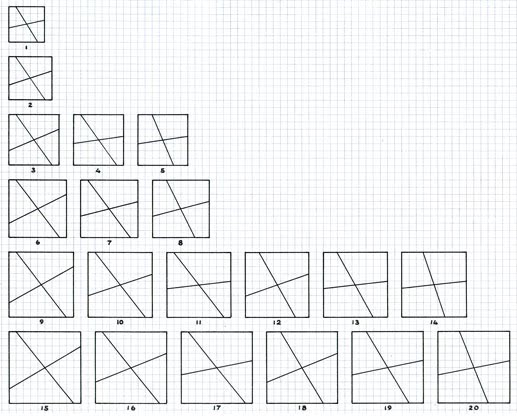
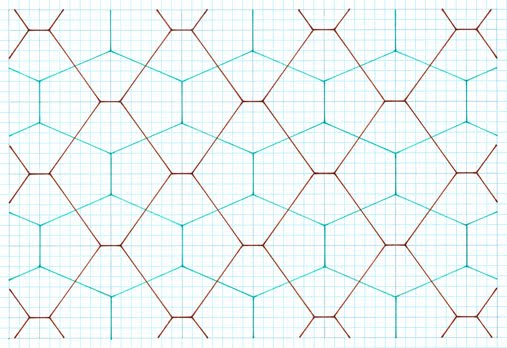
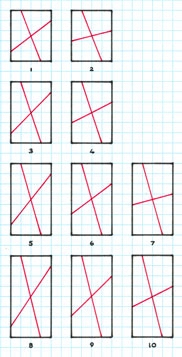
Tilings Upon having shown the premise of
this particular creation, I here show these as actual tilings thereof. Note that for the sake of conciseness, I show just the first
few examples, as there is an infinite number. Exactly, I show five examples, which more than suffices as an indication as to their nature. 1
2
3
4
5 Comments
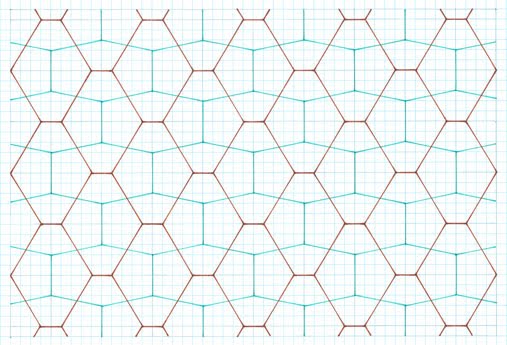
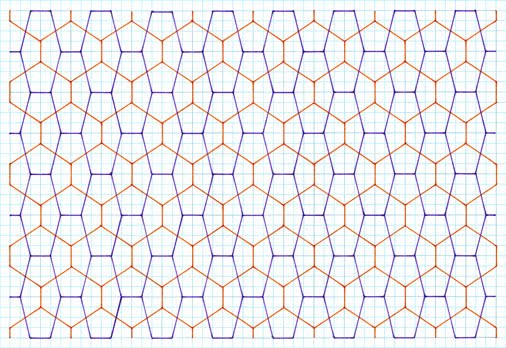
As can be seen, this particular creation
process gives two different pentagons,
both symmetrical. Of interest is that each pentagon has three different side
lengths, of 2, 2, 1 for any given example. Of note is that the angles are no longer
90°, as occurred with the preceding
‘symmetric cross’ of ‘Study 1’.The pentagons range from being two of
very much alike to widely different ones, with decidedly short and long bases
(the ‘1’ side above), of which incidentally can this be described simply as of
short or long bases. Aesthetically, these ‘extreme’ examples are lacking, in
that these are furthest away from an ‘average’ pentagon. The subsidiary
hexagons are at right angles (which as I later show with other, different
premises is not always so) which again is aesthetically pleasing. As can be
seen, as a type, with the increase in number of pentagons, the ‘two pentagon
tilings’ lack the elegance of a single one. Certainly, they are interesting,
but aesthetically pale in comparison.
A variation of the above is with a rectangular format: Premise
This continues with the ‘reflected
stick cross’ premise as in Study 1 , but with a different matrix, namely
that of a rectangle, as according to the intersections of the unit grid. Of
necessity, the resulting stick cross is asymmetric. As can be seen, this
divides the rectangular matrix into four different regions, two of which are
distinct, and so consequently when the rectangular matrix is reflected it thus
gives two different pentagons. As can
be seen, the pentagons are symmetric, of three different side lengths, of 2, 2,
1 proportions for any given tiling. Of note is that the angles are no longer 90° as with Study 1.

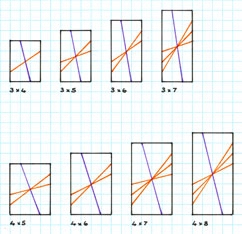
3 x 4 to 3 x 7; 4 x 5 to 4 x 8
3 x 4, 3 x 5, 3 x 6, 3 x 7
4 x 5, 4 x 6, 4 x7, 4 x 8
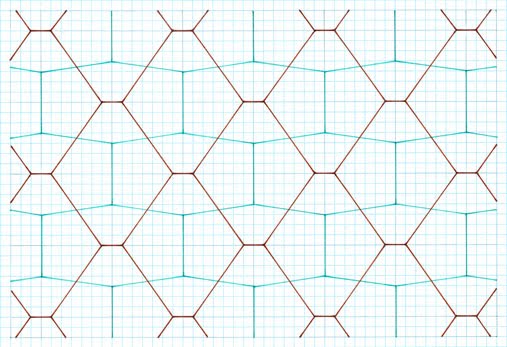
Tilings As above I am
here more circumspect in the number of tilings I show – just three. The reason
for this is that I consider this particular premise, of rectangle grids, as
lacking in aesthetics (see Comments), of which I see no
need to show these to the same depth as with preceding studies, of 18 examples.
Broadly, a few suffice to show the general principle, and so as they are labour
intensive to draw, for reasons of both time saving and their lack of aesthetic
appeal, further examples are not shown.
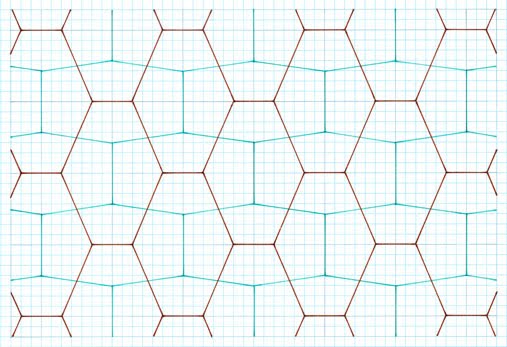
1
2
2
Comments
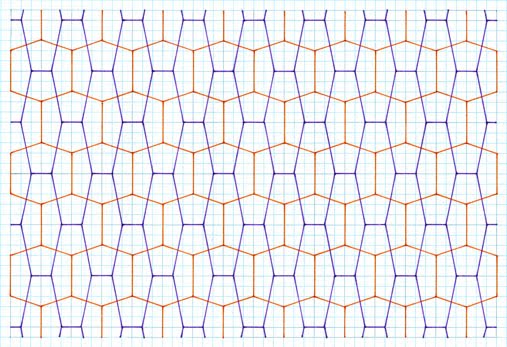
As can be seen, this particular
creation process gives two different
pentagons, both symmetrical. Of interest is that each pentagon has three
different side lengths, of 2, 2, 1 proportions for any given example. Of note
is that the angles are no longer 90°,
as occurred with the preceding Study 1 - ‘symmetric cross and square matrix’. The
pentagons range from being two of broadly alike to widely different ones, with
decidedly short and long bases (the ‘1’ side above), of which incidentally can
this be described simply as of short or long bases. Aesthetically, these
‘extreme’ examples are lacking, in that these are furthest away from an
‘average’ pentagon. The subsidiary hexagons are at right angles (which as I
later show with other, different premises is not always so) which again is
aesthetically pleasing.
Typically, due
to the nature of the (rectangular) matrix, with increasing unit size of the
matrix; 3 x 4, 3 x 5, 3 x 6… this thus results in long, narrow pentagons, the
aesthetics of which are lacking (of which I discuss below). This being so, I
did not pursue further examples, although I do show these in a theoretical
sense, with the construction premise.
As can be
seen, as a type, with the increase in number of pentagons, the ‘two pentagon
tilings’ lack the elegance of a single one. Furthermore, due to the rectangular
matrix, the pentagons are typically ‘elongated’, and so lack appeal. In effect,
these can be regarded as ‘stretched’ squares, and so of limited interest
aesthetically. Certainly, they are, loosely, ‘interesting’, but aesthetically
pale in comparison with other Cairo
tilings, even within the ‘two pentagon’ category.
Another aspect
to this is that although of a different construction to the preceding Study 2 (two
pentagon examples) i.e. square, as against rectangle, the same outcome as to
the ‘type’ of tiling occurs, i.e. 2 pentagons, both symmetrical, same
proportions of sides (2, 2, 1), so although composed differently, they are of
the same ‘type’.
In essence,
this study is lacking in aesthetics (at least in comparison to the related
procedures of Study 1. Firstly, it is composed of two pentagons,
whereas one is aesthetically better. Secondly, the matrix is no longer of the
most basic type of quadrilateral, a square, but of a rectangle. Created 12 September 2011 |